yoshi-camp 2022 winter 参加記 (量子コンピュータ編)
序文 §
yoshi-camp参加記&復習シリーズ2回目はpwnyaaさんによる「猫たちと学ぶ量子コンピュータ」を扱います。
なお、このシリーズが何かについては前回の記事の冒頭を御覧ください。
Prerequisites §
当日の講義では、量子ビットや量子ゲートやテンソル積等の量子計算に関する基本的な知識から教えていただきましたが、それらを全て書いていると時間が幾らあっても足りないので、その辺は賢い読者の皆様の知識や検索能力に委ねます。
また、量子状態は量子ビットを並べて表現しますが、特に断りがなければ一番右側のビットのインデックスを0とし、左に向かってインデックスが大きくなっていくものとします。
量子テレポーテーション §
未知の量子状態と全く同じ量子状態を「複製」する事は出来ないという有名な定理(量子複製不可能定理)が存在しますが、ある量子ビットの状態を別の量子ビットに「移す」事は可能であり、これを量子テレポーテーションと言います。
量子もつれ §
量子テレポーテーションで用いられる概念に量子もつれがあります。これは複数の量子ビットを個別ビットのテンソル積で表せないような状態で、例えば次のようなもの(ベル状態)が代表的です。
$$ \frac 1{\sqrt 2}(\ket{00} + \ket{11}) $$
左側のqubitを観測して0だった場合、右側のqubitが1である事は有り得ず、必ず0になります。同様に左側のqubitを観測して1だった場合、右側のqubitは必ず1になります。量子テレポーテーションではこの状態を用いるため、この状態を作る必要がありますが、これはH, CNOTゲートを用いて簡単に作る事が出来ます(なお、$\mapsto_U$で、ゲート$U$を量子状態に作用させることを指し、ゲートに添え字が付いている場合はその量子ビットに対して作用させることを指します)。
$$ \begin{aligned} \ket{00} &\mapsto_{\mathrm{H}_0} \frac 1{\sqrt 2} (\ket{00} + \ket{01}) \cr &\mapsto_{\mathrm{CNOT}_{0,1}} \frac 1{\sqrt 2}(\ket{00} + \ket{11}) \end{aligned} $$
ここで、$\mathrm{CNOT}_{i,j}$は$i$番目のqubitを制御ビットとして、$j$番目のビットを反転させるCNOTゲートを意味します。
アルゴリズム: 量子テレポーテーション §
AliceとBob間の量子テレポーテーションとして、Aliceが持っている量子状態$\ket{\psi} := \alpha \ket 0 + \beta \ket 1$をBobの持っている量子ビット$q_1$に転送する事を考えます。
まず、AliceとBobでベル状態を分配します。これは次の式のように、Aliceは$\ket \psi$とは別の量子ビット$q_0$に、Bobは量子ビット$q_1$に分配します。
$$ \ket{q_0q_1} = \frac 1{\sqrt 2}(\ket{00} + \ket{11}) $$
続いて$\ket \psi$を制御ビットとして$\ket{q_0}$にCNOTを適用します。その後$\ket \psi$にHを適用します。この地点で系全体の量子状態$\ket{\psi q_0 q_1}$は次のようになります。
$$ \begin{aligned} &\mathrm{H}_\psi\cdot \mathrm{CNOT}_{\psi, q_0}(\ket \psi\ket {q_0 q_1}) \cr &= \frac 1{\sqrt 2}\mathrm{H}_\psi\cdot \mathrm{CNOT}_{\psi, q_0}(\alpha\ket {000} + \alpha \ket{011} + \beta \ket {100} + \beta \ket{111}) \cr &= \frac 1{\sqrt 2}\mathrm{H}_{\psi}(\alpha \ket{000} + \alpha \ket{011} + \beta \ket{110} + \beta \ket{101}) \cr &= \frac 12 (\alpha (\ket{000} + \ket{100} + \ket{011} + \ket{111}) + \beta(\ket{010} - \ket{110} + \ket{001} - \ket{101})) \cr \end{aligned} $$
Aliceは$\ket \psi, \ket {q_0}$を観測します。例えば$\ket \psi \ket {q_0} = \ket{00}$の時、上式の一番下において$\alpha \ket{000}, \beta \ket{001}$の項に対応することから、$\ket{q_1} = \alpha \ket 0 + \beta \ket 1$になります。これを$\ket{00}, \ket{01}, \ket{10}, \ket{11}$の全てにおいて考えると、$\ket{\psi}\ket{q_0}$と$\ket{q_1}$に次のような対応があります。
- $\ket{\psi}\ket{q_0} = \ket{00} \Rightarrow \ket{q_1} = \alpha \ket 0 + \beta \ket 1$
- $\ket{\psi}\ket{q_0} = \ket{01} \Rightarrow \ket{q_1} = \alpha \ket 1 + \beta \ket 0$
- $\ket{\psi}\ket{q_0} = \ket{10} \Rightarrow \ket {q_1} = \alpha \ket 0 - \beta \ket 1$
- $\ket{\psi}\ket{q_0} = \ket{11} \Rightarrow \ket{q_1} = \alpha \ket 1 - \beta \ket 0$
というわけで、4つの観測結果に対して$\ket {q_1}$が異なる状態になることから、その結果に応じてBob側が自分の量子ビット$\ket{q_1}$に対応する量子ゲートを掛ければ$\ket{q_1} = \alpha \ket{0} + \beta \ket{1}$となります。例えば$\ket{\psi}\ket{q_0} = \ket{00}$の場合は既に$\ket{q_1} = \alpha\ket 0 + \beta \ket 1$となっているため、特に量子ゲートを適用させる必要はありません(恒等変換を施すとも言える)。一方、$\ket{\psi}\ket{q_0} = \ket{01}$の場合は、得たい状態に対してビットが反転した状態になっていることから、Xゲートを全体に掛けることになります。他2つの場合はそれぞれZ, ZXゲートを用います。
注意点として「AliceがBobに観測結果を伝えるのは古典ビットを介して行う」という事があります。したがって、名前にテレポーテーションと付いてはいますが、観測結果を得たら瞬時に状態が確定するというだけで「光速を超えて量子状態を転送出来るわけではない」です。
というわけでこれをqiskitで実装したものが次のコードです。当日配布された雛形コードを元に実装しました。
import numpy as np
from qiskit import QuantumCircuit, Aer, assemble
from qiskit.providers.aer import QasmSimulator
from qiskit.quantum_info import partial_trace
ALICE, BOB, MESSAGE = 0, 1, 2
MEASURE_MESSAGE, MEASURE_ALICE = 0, 1
psi = np.array([np.random.rand() + np.random.rand() + 1j,
np.random.rand() + np.random.rand() + 1j])
psi = psi / np.linalg.norm(psi)
print("psi (alice):", psi)
# 3量子2古典ビット / q2はランダムな状態に初期化
qc = QuantumCircuit(3, 2)
qc.initialize(psi, [2])
#**********#
# ここを記述 #
#**********#
# 量子もつれを作る
qc.barrier(label="start implementation")
qc.h(ALICE)
qc.cnot(ALICE, BOB)
qc.cnot(MESSAGE, ALICE)
qc.h(MESSAGE)
qc.barrier(label="implemeted")
#**********#
# ここまで #
#**********#
# アリス側が持っている量子ビットを測定
qc.measure([MESSAGE, ALICE], [MEASURE_MESSAGE, MEASURE_ALICE])
# ボブは結果に応じてX,Zを適用
qc.x(BOB).c_if(MEASURE_ALICE, 1)
qc.z(BOB).c_if(MEASURE_MESSAGE, 1)
# 状態ベクトルを保存
qc.save_statevector()
print(qc.draw())
# ボブ側に転送された状態を確認
svsim = Aer.get_backend('aer_simulator')
qobj = assemble(qc)
res = svsim.run(qobj, shots=1).result()
state_vector = res.get_statevector()
print(state_vector)
実行結果は次のようになります。
psi (alice): [0.71065705+0.40853807j 0.40144718+0.40853807j]
start implementation ┌───┐ ┌───┐ implemeted ┌─┐ statevector
q_0: ───────────────────────────────────────────────────────────░───────────┤ H ├──■──┤ X ├──────────░─────────┤M├────────────────────────────░──────
░ └───┘┌─┴─┐└─┬─┘ ░ └╥┘ ┌───┐ ┌───┐ ░
q_1: ───────────────────────────────────────────────────────────░────────────────┤ X ├──┼────────────░──────────╫────┤ X ├──────┤ Z ├─────────░──────
┌───────────────────────────────────────────────┐ ░ └───┘ │ ┌───┐ ░ ┌─┐ ║ └─╥─┘ └─╥─┘ ░
q_2: ┤ Initialize(0.71066+0.40854j,0.40145+0.40854j) ├──────────░───────────────────────■──┤ H ├─────░──────┤M├─╫──────╫──────────╫───────────░──────
└───────────────────────────────────────────────┘ ░ └───┘ ░ └╥┘ ║ ┌────╨────┐┌────╨────┐ ░
c: 2/════════════════════════════════════════════════════════════════════════════════════════════════════════╩══╩═╡ c_1=0x1 ╞╡ c_0=0x1 ╞═════════════
0 1 └─────────┘└─────────┘
/home/xornet/yoshicamp/quantum/enshu/c3/3-2.py:51: DeprecationWarning: Using a qobj for run() is deprecated as of qiskit-aer 0.9.0 and will be removed no sooner than 3 months from that release date. Transpiled circuits should now be passed directly using `backend.run(circuits, **run_options).
res = svsim.run(qobj, shots=1).result()
Statevector([0.71065705+0.40853807j, 0. +0.j ,
0.40144718+0.40853807j, 0. +0.j ,
0. +0.j , 0. +0.j ,
0. +0.j , 0. +0.j ],
dims=(2, 2, 2))
回路全体は見切れていてますが、Aliceが持っていた$\ket \psi$がpsi (alice): [0.71065705+0.40853807j 0.40144718+0.40853807j]であったのに対して、出力結果の下部にStatevectorとしてこれが現れていることがわかります。
量子ゲートテレポーテーション §
前述の量子テレポーテーションではある量子ビットの状態を別の量子ビットに転送するという事を行いましたが、今度は量子ゲートで似たような事を行えないかを考えます。問題設定としてはAliceの持っている量子ゲート$U$をBobの持っている量子状態$\ket{\psi} := \alpha \ket{0} + \beta \ket{1}$に適用した状態$U\ket{\psi}$をAliceが得たい、というものです。
まずAliceはHゲートを用いて$\ket + = \frac 1{\sqrt 2} (\ket 0 + \ket 1)$を用意します。Aliceの量子ビットを制御ビットとしてBobの量子ビットに対してCNOTゲートを掛けます。(後の問題の都合上、)Aliceの量子ビットのインデックスを1、Bobの量子ビットのインデックスを0とすると次のようになります。
$$ \begin{aligned} \frac 1{\sqrt 2}\mathrm{CNOT}_{1,0}(\ket 0 + \ket 1) (\alpha\ket 0 + \beta\ket 1) \cr = \frac 1{\sqrt 2} (\alpha \ket {00} + \alpha \ket {11} + \beta \ket{01} + \beta \ket{10}) \cr \end{aligned} $$
Aliceは自分の量子ビットにUを掛けます。これで系全体は次のような状態になります。
$$ \begin{aligned} &\mapsto_{U_1} \frac 1{\sqrt 2} {\alpha (U\ket 0) \ket 0 + \alpha (U\ket 1) \ket 1 + \beta (U \ket 0)\ket 1) + \beta (U \ket 1) \ket 0} \cr &= \frac 1{\sqrt 2} {U(\alpha \ket 0 + \beta \ket 1) \ket 0 + U(\alpha \ket 1 + \beta \ket 0) \ket 1} \end{aligned} $$
Bobは自分のビットを測定した結果をAliceに送信します。この状態からわかるようにもしBobが$\ket 0$を観測したら、Aliceのビットは$U(\alpha \ket 0 + \beta \ket 1)$であり、もしBobが$\ket 1$を観測したら、Aliceのビットは$U(\alpha \ket 1 + \beta \ket 0)$になっています。というわけで、量子テレポーテーションの時と同様にして、AliceはBobから得た結果を元に自分のビットへ掛けるゲートを選択すれば、自分のビットで$U(\alpha \ket 0 + \beta \ket 1)$が得られます。$\ket 0$という結果を得たら恒等変換を、$\ket 1$を得たら、$UXU^\dagger$を掛ければ良いです。
BSides Ahmedabad CTF 2021 - qunknown §
以上の手順をそっくりそのまま実装する、という問題が"BSides Ahmedabad CTF 2021 - qunknown"です。次のようなソースコードが与えられます。
import os
import numpy
from qulacs import QuantumState, QuantumCircuit
from qulacs.gate import *
def challenge():
# Create a random gate
dx, dy, dz = [numpy.random.rand()*numpy.pi] * 3
def U(index):
return merge(merge(RX(index, dx), RY(index, dy)), RZ(index, dz))
def Udag(index):
return merge(merge(RZ(index, -dz), RY(index, -dy)), RX(index, -dx))
GATES = {
'CNOT': (CNOT, 2),
'H': (H, 1), 'X': (X, 1), 'Y': (Y, 1), 'Z': (Z, 1),
'S': (S, 1), 'SDAG': (Sdag, 1), 'T': (T, 1), 'TDAG': (Tdag, 1),
'U': (U, 1), 'UDAG': (Udag, 1)
}
CONSUMED = set() # We don't have enough resources :(
def assemble_circuit(asm, qbits=2):
""" Convert assembly into quantum circuit
i.e. q0 ---+--[Z]--
| <= "CNOT 0,1; Z 0; H 1;"
q1 --[X]-[H]--
"""
class QasmException(Exception):
pass
def apply(gate, args):
return gate(*args)
circuit = QuantumCircuit(qbits)
cnt = 0
for instruction in asm.replace('\n', '').split(';'):
t = instruction.strip().split()
if t == []:
continue
if len(t) < 2:
raise QasmException("Invalid instruction")
opecode, operand = t[0].upper(), t[1:]
if opecode not in GATES:
raise QasmException("Invalid gate")
if opecode in CONSUMED:
raise QasmException("Lack of gate")
operand = list(map(lambda x: int(x), ''.join(t[1:]).split(',')))
if not all(map(lambda x: 0 <= x < qbits, operand)):
raise QasmException("Invalid quantum bit specified")
if GATES[opecode][1] != len(operand):
raise QasmException("Invalid number of operands")
CONSUMED.add(opecode)
gate = apply(GATES[opecode][0], operand)
circuit.add_gate(gate)
cnt += 1
if cnt > 100:
raise QasmException("Too large circuit")
return circuit
# 2-bit quantum state
state = QuantumState(2)
state.set_zero_state()
# Randomize 1st qubit (|0>|0> --> |phi>|0>)
RX(0, numpy.random.rand()*numpy.pi).update_quantum_state(state)
RY(0, numpy.random.rand()*numpy.pi).update_quantum_state(state)
RZ(0, numpy.random.rand()*numpy.pi).update_quantum_state(state)
answer_state = state.copy()
# Apply U gate to 1st qubit (answer_state)
U(0).update_quantum_state(answer_state)
# p0 is the probability that 1st qubit is measured to be 0
p0 = answer_state.get_marginal_probability([0, 2])
# Execute your pre-processor (state)
# You can change the state before measurement
asm = input("Pre-processor: ")
circ_pre = assemble_circuit(asm)
circ_pre.update_quantum_state(state)
# Apply U gate to 2nd qubit (state)
U(1).update_quantum_state(state)
# Measure and destroy 1st qubit (state)
Measurement(0, 0).update_quantum_state(state)
print("Measure: " + str(state.get_classical_value(0)))
# Execute your post-processor (state)
# Your goal is to create U|phi> after you measure |phi>
asm = input("Post-processor: ")
circ_post = assemble_circuit(asm)
circ_post.update_quantum_state(state)
# p1 is the probability that 2nd qubit is measured to be 0
p1 = state.get_marginal_probability([2, 0])
# Is 2nd qubit U|phi>?
assert numpy.isclose(p0, p1)
if __name__ == '__main__':
for rnd in range(1, 11):
print(f"[ROUND {rnd}/10]")
try:
challenge()
print("[+] Success!!!")
except Exception as e:
print("[-] Failure...")
print(f" {e}")
break
else:
print(os.getenv("FLAG", "Fake{sample_flag}"))
未知の状態$\ket {\psi}$と未知のゲート$U$に対して、$\ket\psi$が乗っている2量子ビットの回路からもう片方のビットに$U\ket\psi$を出現させる事を10回連続で達成できればフラグが得られます。量子テレポーテーションの時とは異なってqulacsが用いられていますが、サーバー側でassemble_circuit関数を用いて良い感じに回路を組んでくれるようなので、この関数の規約に従って先程のアルゴリズムを実装します。
Pre-processorでは$\ket+$の生成とCNOTの適用を行い、Post-Processorでは直前に観測結果が得られているので、これを元にして恒等変換か$UXU^\dagger$を送れば良いです。次のようなコードになります。
from pwn import remote
sc = remote("localhost", 13337)
# fxxk pylance
# (noReturn in `sc.sendline` treats the following codes as unreached)
def send(payload, sc=sc) -> None:
sc.sendline(payload)
for rnd in range(10):
print(f"round: {rnd}")
sc.recvuntil(b": ")
send(b"H 1; CNOT 1,0;")
sc.recvuntil(b"Measure: ")
m = int(sc.recvline())
if m:
send(b"UDAG 1; X 1; U 1")
else:
send(b"UDAG 1; U 1")
sc.interactive()
量子サブルーチン §
続いての章は量子アルゴリズム内でよく用いられる処理をサブルーチンとしてまとめた量子サブルーチンについてでした。後述のGroverのアルゴリズムで用いる振幅増幅に加えて、次のようなものを扱いましたが、全てに説明と実装例を加えていると人生が何周あっても足りないのでこれらの詳細は割愛します。気が向いたら追記するかもしれません(特に量子フーリエ変換)。
- アダマールテスト: ユニタリ行列$U$の固有値が$e^{i\lambda}$である時に$\lambda$を推定する
- テストを繰り返して$\ket 0, \ket 1$が得られる確率の精度を上げていき、その結果から$\lambda$を逆算する
- スワップテスト: 2つのベクトルの内積を計算する
- アダマールテスト同様に$\ket 0$が得られる確率から内積を求める
- 量子フーリエ変換: 離散フーリエ変換を量子回路で実現する
- 量子位相推定: ユニタリ行列$U$とその固有ベクトル$\ket \psi$を受け取って固有値$e^{i2\pi \phi}$の$\phi$を計算する
- アダマールテストと異なり、位相が確率分布ではなく量子状態として得られるので、テストを繰り返すことなく計算する
振幅増幅 §
次のようなオラクル関数$f(x)$を考えます。ここで、$x$はビット列であり、各ビットは直交性があるものとします(ビット列を通常の計算基底$\ket 0, \ket 1$のテンソル積として表せばこれは実現できる)。
$$ f(x) = \begin{cases} 1 & x\mathrm{が解} \cr 0 & \mathrm{otherwise} \end{cases} $$
振幅増幅サブルーチンの入力にとる状態を$\ket \psi$とおきます。この状態に対して、解となる状態が張る部分$\ket \beta$とそれ以外の成分$\ket \alpha$に分けると、何らかの$\theta$が存在して次が成り立ちます。後に再登場するので断っておくと、$\theta$は$\ket\psi$と$\ket\alpha$の間の角となります。
$$ \ket \psi = \cos \theta \ket \alpha + e^{i\phi} \sin \theta \ket \beta $$
通常、問題の解となる状態は少ないことから、普通の量子状態であれば$\ket \beta$が得られる確率は小さくなり、したがって$\sin \theta$は小さくなります。そこで、このサブルーチンでは状態$\ket \psi$の$\theta$を大きくするような回路を構成します。幾何的には$\ket \alpha, \ket \beta$の2つを(直交している)基底とし、$\ket \psi$の$\ket \alpha$を軸とした反転操作$U_\omega$を行った後に反転前の$\ket \psi$を軸とした反転操作$U_\psi$を行い、この2回の反転を繰り返すことで$\ket \beta$に近づける事に対応します。資料の図を(勝手に)拝借すると次のようになっています。
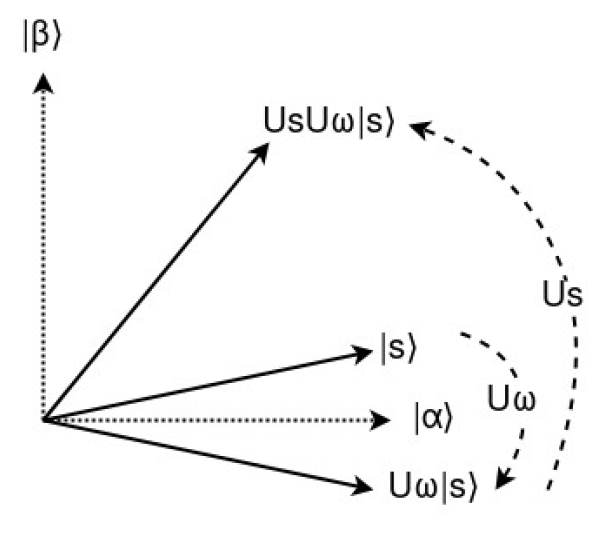
1つ目の反転操作がどのように行列で表現されるかは簡単で$\ket\beta$成分の符号を変えれば良いです。よって$U_\omega$は($\ket\alpha, \ket\beta$を基底として)次のような行列になります。
$$ U_\omega = \begin{pmatrix} 1 & 0 \cr 0 & -1 \end{pmatrix} $$
2つ目の反転操作$U_\psi$(図中では$U_s$)を考えるために、反転したい状態を$\ket \phi$とおいて、これを$\ket\psi$に射影した状態$\ket {\phi'}$を用意します。$\ket{\phi'}$は$\ket \phi$の$\ket \psi$への射影なので$\ket\psi$の定数倍の状態であり、その係数は2つの状態の内積$\braket {\psi | \phi}$であることから次が成り立ちます。
$$ \begin{aligned} \ket {\phi'} &= \ket \psi (\braket {\psi|\phi}) \cr &= (\ket \psi \bra \psi) \ket \phi \end{aligned} $$
この$\ket {\phi'}$を用いると$\ket\psi$軸中心の反転は$\ket \phi$から$\ket {\phi'}$へ「何らかの状態(ベクトル)を足す」という形で移してから、同じ分の状態を足してあげれば良い事になります(ヒント: 図を書く)。というわけで次が成り立ちます。
$$ U_\psi \ket \phi = \phi + 2(\ket {\phi'} - \ket \phi) = 2(\ket\psi \bra\psi)\ket\phi - \ket \phi = (2\ket \psi \bra \psi - I) \ket \phi $$
これより、$U_\psi = 2\ket \psi \bra \psi - I$になります。この行列$U_\psi$は$\ket \psi$と直交する成分を反転させるという性質があります。任意の状態$\ket\phi$を$\ket \psi$とその直交成分$\ket {\psi^\perp}$に分解して$\ket \phi = \alpha \ket \psi + \beta \ket {\psi^\perp} \ (\alpha^2 + \beta^2 = 1)$のようにおくと次が成り立ちます。
$$ \begin{aligned} U_\psi\ket \phi &= \alpha(2\ket \psi \bra \psi - I) \ket \psi + \beta(2\ket \psi \bra \psi - I) \ket {\psi^\perp} \cr &= \alpha(2\ket \psi - \ket\psi) - \beta \ket {\psi^\perp} \cr &= \alpha \ket \psi - \beta \ket {\psi^\perp} \end{aligned} $$
この結果から、$U_\psi$が$\ket\psi$と直交する成分の符号を反転させる事がわかります。このことからも$U_\psi$が$\ket\psi$を中心軸としてベクトルを反転させるということがわかります。
ところで、この2つの反転操作ははじめに$\ket \psi$を$-2\theta$回転させた後に$4\theta$回転させていることになります。したがって、$\ket\psi$の$\alpha$に対する角度$\theta$はこの一連の操作によって$2\theta$増えることから、$U_\psi U_\omega$を$k$回繰り返した場合に関して次が成り立ちます1。
$$ (U_\psi U_\omega)^k \ket \psi = \cos(2k +1)\theta\ket \alpha + e^{i\phi}\sin(2k + 1)\theta \ket \beta $$
というわけで$\cos(2k+1)\theta$が出来るだけ1に近づくような$k$に対して$k$回この操作を行えば良いです。したがって、効率の良い$k$を求めるためには$\theta$が既知である必要があります。
振幅増幅をnumpyとqiskitを用いて実装したのが次の通りです。$\ket\psi$として次のような場合を考え、$\ket{11}$が観測される確率を増やすという状況です。
$$ \ket \psi = \frac 1{\sqrt 5} \ket{01} + \frac 1{\sqrt 5} \ket {10} + \sqrt{\frac 35} \ket{11} $$
import numpy as np
from qiskit import QuantumCircuit, transpile
from qiskit.circuit.library.standard_gates import TGate
from qiskit.providers.aer import QasmSimulator
from qiskit.quantum_info.operators import Operator
inv_sqrt_5 = 1 / np.sqrt(5)
psi = np.matrix([
[0],
[inv_sqrt_5],
[inv_sqrt_5],
[np.sqrt(3/5)]
])
# beta = |11>
beta = np.matrix([
[0],
[0],
[0],
[1]
])
I = np.identity(4)
U_w = Operator(I - 2 * beta * beta.transpose())
U_s = Operator(2*psi * psi.transpose() - I)
# print(U_w)
# print(U_s)
def amplify(k):
qc = QuantumCircuit(2, 2)
qc.initialize(np.squeeze(np.asarray(psi)), qc.qubits)
for _ in range(k):
qc.append(U_w, qc.qubits)
qc.append(U_s, qc.qubits)
qc.measure(qc.qubits, qc.clbits)
# print(qc.draw())
sim = QasmSimulator()
cqc = transpile(qc, sim)
job = sim.run(cqc, shots=10000)
cnt = job.result().get_counts()
res = cnt['11'] / 10000
return res
# search better k
for k in range(200):
try:
res = amplify(k)
if res > 0.9:
print(k, res)
except:
pass
量子アルゴリズム §
続く量子アルゴリズムの章では前述のサブルーチンを用いて特定の問題を解くアルゴリズムを扱いました。その中でも特に有名なShorのアルゴリズムについては、講義で理論をさらって演習は特に設けられなかったので割愛し2、Groverのアルゴリズムを用いてSATを解く方法について書きます。
Groverのアルゴリズム (を用いてSATを解く) §
先程登場した振幅増幅を用いて解状態が出現する確率を上げてから測定を行って解を求めるアルゴリズムがGroverのアルゴリズムです。オラクルをユニタリ行列$U_\omega$として表せる問題に対して有効で、講義ではSATを扱いました。
初期状態は$\ket s$として$\ket s := H^{\otimes n} \ket {00 \cdots 0}$のように作ります。この全ての状態が平等に出るような状態から解の状態だけ振幅を増幅させて観測確率を上げます。
$U_\omega$は量子状態が解と一致としている場合に位相を反転させるという役割であることから、SATの場合はCNOTをn個の制御ビットに拡張させたn-Toffoliゲートを用いると上手くいきます。
例えば$\lnot x_0 \lor x_1 \lor \lnot x_2$という節は$\lnot(x_0 \land \lnot x_1 \land x_2)$と同値になるため$\ket{101}$という状態は解では無いことがわかります。よってこの解では無い状態をマークする次のような回路として、0,2ビット目が1、1ビット目が0の時に反転する制御NOTゲートを考え、これを用いて補助ビットを反転させます。これを節の数だけ補助ビットを用意して同様の事を行い、補助ビットが「全て0の時に」位相を反転するような回路を考えてやればいいです。最も簡単なものは制御ビットを補助ビットとして考え、全て0の時にNOTをかけたら位相が反転してくれるような別の補助ビットを用意しておくことです。これには$\ket - := HX\ket 0 = \frac 1{\sqrt 2}(\ket 0 - \ket 1)$が使えます。$\ket -$に関して次が成り立っていることを確認しておきます。
$$ X\ket - = X \frac 1{\sqrt 2}(\ket 0 - \ket 1) = \frac 1{\sqrt 2}(\ket 1 - \ket 0) = -\ket - $$
実際に$(x_0 \lor x_1) \land (\lnot x_0 \lor x_2) \land (x_1 \lor \lnot x_2) \land (\lnot x_1 \lor x_2)$に対応するオラクルを考えてみると次のようになります。$q_0, q_1, q_2$が$x_0, x_1, x_2$に対応する量子ビットで、$q_3,q_4,q_5,q_6$が各節に対応する制御ビット、$q_7$がグローバル位相に対応する量子ビット($HX \ket 0 = \ket -$に初期化されている)となります。
┌───┐
q_0: ┤ H ├──o────■─────────────────
├───┤ │ │
q_1: ┤ H ├──o────┼────o────■───────
├───┤ │ │ │ │
q_2: ┤ H ├──┼────o────■────o───────
└───┘┌─┴─┐ │ │ │
q_3: ─────┤ X ├──┼────┼────┼────o──
└───┘┌─┴─┐ │ │ │
q_4: ──────────┤ X ├──┼────┼────o──
└───┘┌─┴─┐ │ │
q_5: ───────────────┤ X ├──┼────o──
└───┘┌─┴─┐ │
q_6: ────────────────────┤ X ├──o──
┌───┐┌───┐ └───┘┌─┴─┐
q_7: ┤ X ├┤ H ├───────────────┤ X ├
└───┘└───┘ └───┘
ところで、振幅増幅は1回だけ行われるとは限らず繰り返される事があります。このままでは、$q_7$以外の制御ビットが反転されたままですので逆順に節に対応する制御ゲートを再度かけてあげて元に戻す必要があります。
┌───┐
q_0: ┤ H ├──o────■─────────────────────────────■────o──
├───┤ │ │ │ │
q_1: ┤ H ├──o────┼────o────■─────────■────o────┼────o──
├───┤ │ │ │ │ │ │ │ │
q_2: ┤ H ├──┼────o────■────o─────────o────■────o────┼──
└───┘┌─┴─┐ │ │ │ │ │ │ ┌─┴─┐
q_3: ─────┤ X ├──┼────┼────┼────o────┼────┼────┼──┤ X ├
└───┘┌─┴─┐ │ │ │ │ │ ┌─┴─┐└───┘
q_4: ──────────┤ X ├──┼────┼────o────┼────┼──┤ X ├─────
└───┘┌─┴─┐ │ │ │ ┌─┴─┐└───┘
q_5: ───────────────┤ X ├──┼────o────┼──┤ X ├──────────
└───┘┌─┴─┐ │ ┌─┴─┐└───┘
q_6: ────────────────────┤ X ├──o──┤ X ├───────────────
┌───┐┌───┐ └───┘┌─┴─┐└───┘
q_7: ┤ X ├┤ H ├───────────────┤ X ├────────────────────
└───┘└───┘ └───┘
残すは$U_s$の設計です。振幅増幅の箇所で述べたように$U_s = 2\ket s \bra s - I$であり、$\ket s$と直交する成分の位相を反転させます。ここで、$\ket s = H^{\otimes n}\ket {0^{\otimes n}}$であることからアダマールゲートを用いて$\ket s \mapsto \ket {0^{\otimes n}}$と変換してから$\ket {0^{\otimes n}}$以外の位相を反転させて再び$H^{\otimes n}$で戻して上げれば良いです。途中の反転するゲートは$U_\omega$でも用いた「制御ビットが全てが0の時にNOTゲートで$\ket -$の位相を反転させる」ゲートを用います。
$U_\omega, U_s$を合わせると最終的に次のような増幅回路が出来上がります。
┌───┐ ┌───┐ ┌───┐
q_0: ┤ H ├──o────■─────────────────────────────■────o──┤ H ├──o──┤ H ├
├───┤ │ │ │ │ ├───┤ │ ├───┤
q_1: ┤ H ├──o────┼────o────■─────────■────o────┼────o──┤ H ├──o──┤ H ├
├───┤ │ │ │ │ │ │ │ │ ├───┤ │ ├───┤
q_2: ┤ H ├──┼────o────■────o─────────o────■────o────┼──┤ H ├──o──┤ H ├
└───┘┌─┴─┐ │ │ │ │ │ │ ┌─┴─┐└───┘ │ └───┘
q_3: ─────┤ X ├──┼────┼────┼────o────┼────┼────┼──┤ X ├───────┼───────
└───┘┌─┴─┐ │ │ │ │ │ ┌─┴─┐└───┘ │
q_4: ──────────┤ X ├──┼────┼────o────┼────┼──┤ X ├────────────┼───────
└───┘┌─┴─┐ │ │ │ ┌─┴─┐└───┘ │
q_5: ───────────────┤ X ├──┼────o────┼──┤ X ├─────────────────┼───────
└───┘┌─┴─┐ │ ┌─┴─┐└───┘ │
q_6: ────────────────────┤ X ├──o──┤ X ├──────────────────────┼───────
┌───┐┌───┐ └───┘┌─┴─┐└───┘ ┌─┴─┐
q_7: ┤ X ├┤ H ├───────────────┤ X ├─────────────────────────┤ X ├─────
└───┘└───┘ └───┘ └───┘
あとは適当な回数(但しこの例では1回)増幅して$q_0, q_1, q_2$を測定した結果から有意な回数出ている状態がSATの解に対応します。これをQiskitで実装すると次のようになります。
from qiskit.circuit.library.standard_gates import XGate
from qiskit import QuantumCircuit, transpile
from qiskit.providers.aer import QasmSimulator
qc = QuantumCircuit(3 + 4 + 1, 3)
qc.x(7)
qc.h(7)
qc.h(0)
qc.h(1)
qc.h(2)
# 2->制御ビットの個数
# ctrl_state='001' --> 回路図の上のビットから順に黒丸、白丸、白丸
# [0,1,3] --> [0,1]が制御ビット、[3]がターゲットビット
qc.append(XGate().control(2, ctrl_state='00'), [0,1,3])
qc.append(XGate().control(2, ctrl_state='01'), [0,2,4])
qc.append(XGate().control(2, ctrl_state='10'), [1,2,5])
qc.append(XGate().control(2, ctrl_state='01'), [1,2,6])
qc.append(XGate().control(4, ctrl_state='0000'), [3,4,5,6,7])
qc.append(XGate().control(2, ctrl_state='01'), [1,2,6])
qc.append(XGate().control(2, ctrl_state='10'), [1,2,5])
qc.append(XGate().control(2, ctrl_state='01'), [0,2,4])
qc.append(XGate().control(2, ctrl_state='00'), [0,1,3])
qc.h(0)
qc.h(1)
qc.h(2)
qc.append(XGate().control(3, ctrl_state="000"), [0,1,2,7])
qc.h(0)
qc.h(1)
qc.h(2)
qc.measure([0,1,2], qc.clbits)
print(qc.draw())
sim = QasmSimulator()
cqc = transpile(qc, sim)
job = sim.run(cqc, shots=10000)
cnt = job.result().get_counts()
print(cnt)
実行結果は次のようになります。
┌───┐ ┌───┐ ┌───┐┌─┐
q_0: ┤ H ├──o────■─────────────────────────────■────o──┤ H ├──o──┤ H ├┤M├──────
├───┤ │ │ │ │ ├───┤ │ ├───┤└╥┘┌─┐
q_1: ┤ H ├──o────┼────o────■─────────■────o────┼────o──┤ H ├──o──┤ H ├─╫─┤M├───
├───┤ │ │ │ │ │ │ │ │ ├───┤ │ ├───┤ ║ └╥┘┌─┐
q_2: ┤ H ├──┼────o────■────o─────────o────■────o────┼──┤ H ├──o──┤ H ├─╫──╫─┤M├
└───┘┌─┴─┐ │ │ │ │ │ │ ┌─┴─┐└───┘ │ └───┘ ║ ║ └╥┘
q_3: ─────┤ X ├──┼────┼────┼────o────┼────┼────┼──┤ X ├───────┼────────╫──╫──╫─
└───┘┌─┴─┐ │ │ │ │ │ ┌─┴─┐└───┘ │ ║ ║ ║
q_4: ──────────┤ X ├──┼────┼────o────┼────┼──┤ X ├────────────┼────────╫──╫──╫─
└───┘┌─┴─┐ │ │ │ ┌─┴─┐└───┘ │ ║ ║ ║
q_5: ───────────────┤ X ├──┼────o────┼──┤ X ├─────────────────┼────────╫──╫──╫─
└───┘┌─┴─┐ │ ┌─┴─┐└───┘ │ ║ ║ ║
q_6: ────────────────────┤ X ├──o──┤ X ├──────────────────────┼────────╫──╫──╫─
┌───┐┌───┐ └───┘┌─┴─┐└───┘ ┌─┴─┐ ║ ║ ║
q_7: ┤ X ├┤ H ├───────────────┤ X ├─────────────────────────┤ X ├──────╫──╫──╫─
└───┘└───┘ └───┘ └───┘ ║ ║ ║
c: 3/══════════════════════════════════════════════════════════════════╩══╩══╩═
0 1 2
{'110': 5038, '111': 4962}
$\ket {110}, \ket{111}$が多く得られており、これはそれぞれ$(x_0, x_1, x_2) = (0,1,1), (1,1,1)$に対応します(量子ビットの並びと変数の並びが逆なことに注意)。実際に$(x_0 \lor x_1) \land (\lnot x_0 \lor x_2) \land (x_1 \lor \lnot x_2) \land (\lnot x_1 \lor x_2)$に代入してみると確かに充足解であることがわかります(他の解が無いこともわかる)。
zer0pts CTF 2022 - q-solved §
次のPythonスクリプトと、内部で読み込んでいるcircuit.jsonが渡されます。
import gmpy2
from qiskit import QuantumCircuit, execute, Aer
from qiskit.circuit.library import XGate
import json
with open("circuit.json", "r") as f:
circ = json.load(f)
nq = circ['memory']
na = circ['ancilla']
target = nq + na
print("[+] Constructing circuit...")
main = QuantumCircuit(nq + na + 1, nq)
sub = QuantumCircuit(nq + na + 1)
main.x(target)
main.h(target)
for i in range(circ['memory']):
main.h(i)
t = circ['memory']
for cs in circ['circuit']:
ctrl = ''.join(['0' if x else '1' for (x, _) in cs])
l = [c for (_, c) in cs]
sub.append(XGate().control(len(cs), ctrl_state=ctrl), l + [t])
t += 1
sub.append(XGate().control(na, ctrl_state='0'*na),
[i for i in range(nq, nq + na)] + [target])
for cs in circ['circuit'][::-1]:
t -= 1
ctrl = ''.join(['0' if x else '1' for (x, _) in cs])
l = [c for (_, c) in cs]
sub.append(XGate().control(len(cs), ctrl_state=ctrl), l + [t])
sub.h([i for i in range(nq)])
sub.append(XGate().control(nq, ctrl_state='0'*nq),
[i for i in range(nq)] + [target])
sub.h([i for i in range(nq)])
for i in range(round(0.785 * int(gmpy2.isqrt(2**nq)) - 0.5)):
main.append(sub, [i for i in range(na + nq + 1)])
for i in range(nq):
main.measure(i, i)
print("[+] Calculating flag...")
emulator = Aer.get_backend('qasm_simulator')
job = execute(main, emulator, shots=1024)
hist = job.result().get_counts()
result = sorted(hist.items(), key=lambda x: -x[1])[0][0]
print("[+] FLAG:")
print(int.to_bytes(int(result, 2), nq//8, 'little'))
jsonの方はクソ長いので部分的に表示すると次のようになっています。
{'ancilla': 1408,
'circuit': [[[False, 0]],
[[True, 0], [False, 8], [False, 280]],
[[False, 0], [True, 8], [False, 280]],
[[True, 280], [False, 0], [False, 8]],
[[True, 0], [True, 8], [True, 280]],
~~ snipped ~~
[[False, 558]],
[[False, 7], [False, 279], [False, 559]],
[[True, 7], [True, 279], [False, 559]],
[[False, 7], [True, 279], [True, 559]],
[[True, 7], [False, 279], [True, 559]],
[[False, 559]]],
'memory': 560}
どうやらこのスクリプトは先程紹介したGroverのアルゴリズムを用いてSATを解いているようです。というわけで配布スクリプトを実行すれば終わり……なはずがありません。というのも量子ビットの数に関して次のような記述があります。
nq = circ['memory']
na = circ['ancilla']
target = nq + na
print("[+] Constructing circuit...")
main = QuantumCircuit(nq + na + 1, nq)
sub = QuantumCircuit(nq + na + 1)
上記JSONからもわかるようにnq, naはそれぞれ560, 1408です。これだけの量子ビットをシミュレートしようとすると$2^{1968}$次元ぐらいの行列が必要になってメモリを瞬時に食いつぶします。
このままでは解けない問題を渡されて憤慨するところですが、賢いCTFプレイヤーの皆様ならご存知の通り、SATに対する有効なアプローチとして量子アルゴリズムを持ち出さなくともz3というクソ便利なものがあります。というわけでcircuit.jsonがどのように回路に変換されているのかを見て対応する問題をz3を使って解けば良いです。
前述の説明の形式から既にGuessableではありますが、circ['circuit']はCNFが配列として表現されているのでこれをz3にそのままぶち込みます。
import json
import z3
with open("./circuit.json") as f:
j = json.load(f)
circ = j["circuit"]
solver = z3.Solver()
bvs = [z3.Bool(f"x_{i}") for i in range(j["memory"])]
for cs in circ:
or_constraints = []
for b, i in cs:
or_constraints.append(bvs[i] == b)
solver.add(z3.Or(or_constraints))
res = solver.check()
flag = ""
if res == z3.sat:
m = solver.model()
for bv in bvs:
b = m[bv]
flag = ("1" if b else "0") + flag
flag = int(flag, 2).to_bytes(j["memory"] // 8, "little")
print(flag)
else:
print("ha?")
やり残したこと §
講義で扱ったり資料に記載されたりしていましたが、時間の都合等で解かなかった問題が幾つか残っているのでその内やるかもしれません。
- Shorのアルゴリズムの例題 (DiceCTF 2021 - quantum 1, 2)
- 量子鍵交換の例題 (zer0pts CTF 2021 - TokyoNetwork)
次回予告 §
次回はmitsuさんによる「ネコちゃん式 〜安全な楕円曲線の生成〜」の記録と復習について書く予定ですが、扱ったアルゴリズムの難解さとSageMathの複雑怪奇な仕様に苦しんでいるのでいつ終わるかはわかりません。
当日の成果としては、安全な楕円曲線を作るためには位数計算が重要なので、これを計算するSchoofのアルゴリズムを実装しました……という予定だったのですが、主にSageMathがデレてくれなくて一生エラーを吐き続けるせいで講義中に実装を終える事は叶いませんでした。というわけで、これの実装を最低目標とし、その後は計算量が削減されたSEA(Schoof, Elkies, Atkin)アルゴリズムの理解に挑む予定です。
参考文献 §
基本的に当日配布の講義資料を参照しましたが、それ以外にも理解の役に立ったものを載せています。
資料中ではちゃんと代数的に示していたが、数式が多くなってきたので幾何的な説明に留めている
これは言い訳に過ぎず、説明するのが面倒 + 私が量子フーリエ変換をよく理解していないだけです